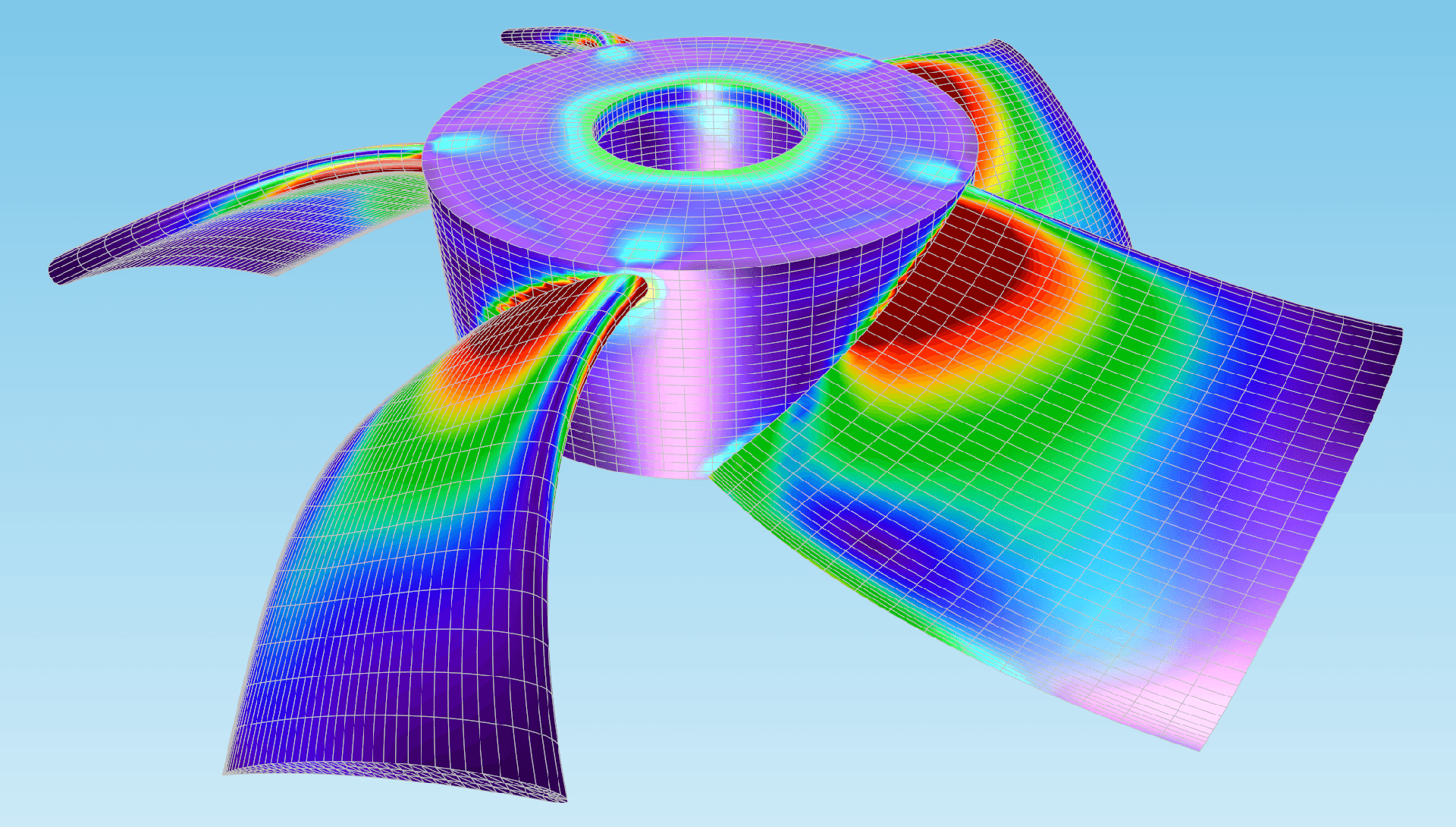
Метод скінченних елементів — це потужний чисельний підхід, який широко використовується для розв’язання складних інженерних та фізичних задач. Він дозволяє моделювати процеси в механіці, будівництві, теплофізиці, електродинаміці та інших галузях, де аналітичні розв’язки неможливі або дуже складні.
Що таке метод скінченних елементів
Метод скінченних елементів (МСЕ, англ. Finite Element Method, FEM) — це чисельний метод розв’язання диференціальних рівнянь, які описують фізичні процеси. Його суть полягає в розбитті області дослідження на невеликі, прості частини — скінченні елементи. У межах кожного елемента функції апроксимуються простими аналітичними виразами, що дозволяє значно спростити обчислення.
Цей метод застосовується для моделювання деформацій твердих тіл, теплопередачі, електричних та магнітних полів, а також у гідродинаміці.
Основні принципи
Основними етапами застосування методу скінченних елементів є:
- Дискретизація області — поділ складної геометрії на простіші елементи (трикутники, чотирикутники, тетраедри тощо).
- Вибір апроксимаційних функцій — визначення функцій, які описують змінні в межах кожного елемента.
- Формулювання слабкої форми рівнянь — перетворення диференціальних рівнянь у форму, придатну для чисельного розв’язання.
- Складання глобальної системи рівнянь — зведення локальних моделей елементів у загальну систему.
- Розв’язання системи — обчислення шуканих значень у вузлах елементів.
- Аналіз результатів — побудова графіків, візуалізація полів напружень, температур тощо.
Типи скінченних елементів
Скінченні елементи поділяються за:
- Розмірністю:
- 1D (стрижневі або балкові елементи),
- 2D (трикутні, чотирикутні елементи),
- 3D (тетраедральні, гексаедральні елементи).
- Типом апроксимації:
- Лінійні,
- Квадратичні,
- Кубічні тощо.
- Призначенням:
- Для аналізу деформацій,
- Для моделювання теплопровідності,
- Для електромагнітного аналізу.
Кожен тип елементів має свої особливості та область застосування, що визначається геометрією задачі та точністю, яку потрібно досягти.
Переваги та недоліки методу
Переваги
- Можливість розв’язання складних геометричних задач;
- Гнучкість при роботі з неоднорідними матеріалами та складними умовами;
- Широка реалізація в програмному забезпеченні (ANSYS, Abaqus, COMSOL тощо);
- Висока точність при достатньому розбитті сітки.
Недоліки
- Високі обчислювальні витрати при великій кількості елементів;
- Потреба у досвідченому користувачі для правильного формулювання задачі;
- Можливі похибки при неправильному виборі сітки або граничних умов.
Метод скінченних елементів залишається одним з найважливіших інструментів інженера-аналітика, незважаючи на його складність та обчислювальні ресурси, що вимагаються.
Джерело:
Zienkiewicz, O. C., & Taylor, R. L. (2005). The Finite Element Method. Elsevier.
https://doi.org/10.1016/B978-0-7506-6320-0.X5000-0